Una ecuación es una igualdad matemática entre dos expresiones algebraicas,denominadas miembros,en las que aparecen valores conocidos o datos,y desconocidos o incógnitas,relacionados mediante operaciones matemáticas.Las incógnitas,representadas generalmente con letras constituyen los valores que se pretenden hallar.El método para resolver una ecuación consiste en ir transformándola,mediante sucesivos pasos,en otras equivalentes mas sencillas hasta despejar la incógnita.

En este vídeo se ve como se hacen las ecuaciones de primer grado
El inventor del algebra,Al Juarismi:

Abu Abdallah Muḥammad ibn Mūsā al-Jwārizmī (Abu Yāffar) (أبو عبد الله محمد بن موسى الخوارزمي ابو جعفر), conocido generalmente como al-Juarismi, fue un matemático,astrónomo y geógrafo persa1 2 musulmán, que vivió aproximadamente entre 780 y850.
Poco se conoce de su biografía, a tal punto que existen discusiones no saldadas sobre su lugar de nacimiento. Algunos sostienen que nació en Bagdad. Otros, siguiendo el artículo de Gerald Toomer3 (a su vez, basado en escritos del historiador al-Tabari) sostienen que nació en la ciudad corasmia de Jiva, en el actual Uzbekistán. Rashed4 halla que se trata de un error de interpretación de Toomer, debido a un error de transcripción (la falta de la conectiva wa) en una copia del manuscrito de al-Tabari. No será este el último desacuerdo entre historiadores que encontraremos en las descripciones de la vida y las obras de al-Juarismi. Estudió y trabajó en Bagdad en la primera mitad del siglo IX, en la corte del califa al-Mamun. Para muchos, fue el más grande de los matemáticos de su época.
Debemos a su nombre y al de su obra principal, "Hisāb al-ŷabr wa'l muqābala", (حساب الجبر و المقابلة) nuestras palabras álgebra, guarismo y algoritmo. De hecho, es considerado como el padre del álgebra y como el introductor de nuestro sistema de numeración denominado arábigo.
Hacia 815 al-Mamun, séptimo califa Abásida, hijo de Harún al-Rashid, fundó en su capital, Bagdad, la Casa de la sabiduría(Bayt al-Hikma), una institución de investigación y traducción que algunos han comparado con la Biblioteca de Alejandría. En ella se tradujeron al árabe obras científicas y filosóficas griegas e indias. Contaba también con observatorios astronómicos. En este ambiente científico y multicultural se educó y trabajó al-Juarismi junto con otros científicos como los hermanos Banu Musa, al-Kindi y el famoso traductor Hunayn ibn Ishaq. Dos de sus obras, sus tratados de álgebra y astronomía, están dedicadas al propio califa.
Ecuaciones de segundo grado:
Una ecuación algebraica de segundo grado1 2 o simplemente ecuación cuadrática de una variable es una ecuación algebraica que conlleva una expresión algebraica de términos cuyo grado máximo es dos, es decir, una ecuación cuadrática puede ser representada por un trinomio de segundo grado o binomio de segundo grado. La expresión general de una ecuación cuadrática de una variable es:

En este vídeo se ve como se hacen las ecuaciones de segundo grado
En este vídeo se ve como se hacen las ecuaciones exponenciales
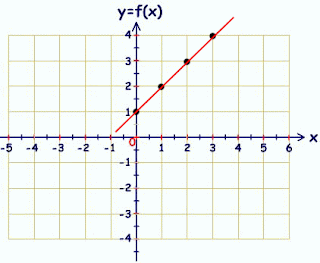
Representación gráfica de rectas
En este vídeo veras como se hacen las funciones lineales
Definición de trigonometria :
La trigonometría es una rama de la matemática, cuyo significado etimológico es 'la medición de los triángulos'. Deriva de los términos griegos τριγωνοϛ trigōnos 'triángulo' y μετρον metron 'medida'.1
En términos generales, la trigonometría es el estudio de las razones trigonométricas: seno, coseno; tangente, cotangente; secante y cosecante. Interviene directa o indirectamente en las demás ramas de la matemática y se aplica en todos aquellos ámbitos donde se requieren medidas de precisión. La trigonometría se aplica a otras ramas de la geometría, como es el caso del estudio de las esferas en la geometría del espacio.
Posee numerosas aplicaciones, entre las que se encuentran: las técnicas de triangulación, por ejemplo, son usadas en astronomía para medir distancias a estrellas próximas, en la medición de distancias entre puntos geográficos, y en sistemas global de navegación por satélites.


En este vídeo veras como se hace una parábola
Estadística:
La estadística es una ciencia formal y una herramienta que estudia el uso y los análisis provenientes de una muestra representativa de datos, busca explicar las correlaciones y dependencias de un fenómeno físico o natural, de ocurrencia en forma aleatoria o condicional.
Sin embargo, la estadística es más que eso, es decir, es la herramienta fundamental que permite llevar a cabo el proceso relacionado de la estadística con la investigación científica.
Es transversal a una amplia variedad de disciplinas, desde la física hasta las ciencias sociales, desde las ciencias de la salud hasta el control de calidad.
Se usa para la toma de decisiones en áreas de negocios o instituciones gubernamentales.
La estadística se divide en dos grandes áreas:
Estadística descriptiva: Se dedica a la descripción, visualización y resumen de datos originados a partir de los fenómenos de estudio. Los datos pueden ser resumidos numérica o gráficamente. Ejemplos básicos de parámetros estadísticos son: la media y la desviación estándar. Algunos ejemplos gráficos son: histograma, pirámide poblacional, gráfico circular, entre otros.
Estadística inferencial: Se dedica a la generación de los modelos, inferencias y predicciones asociadas a los fenómenos en cuestión teniendo en cuenta la aleatoriedad de las observaciones. Se usa para modelar patrones en los datos y extraer inferencias acerca de la población bajo estudio. Estas inferencias pueden tomar la forma de respuestas a preguntas sí/no (prueba de hipótesis), estimaciones de unas características numéricas (estimación), pronósticos de futuras observaciones, descripciones de asociación (correlación) o modelamiento de relaciones entre variables (análisis de regresión). Otras técnicas de modelamiento incluyen análisis de varianza, series de tiempo y minería de datos.
Ambas ramas (descriptiva e inferencial) comprenden la estadística aplicada. La estadística inferencial, por su parte, se divide en estadística paramétrica y estadística no paramétrica.
Hay también una disciplina llamada estadística matemática, la que se refiere a las bases teóricas de la materia.
La palabra «estadísticas» también se refiere al resultado de aplicar un algoritmo estadístico a un conjunto de datos, como en estadísticas económicas, estadísticas criminales, entre otros.
Vídeo de introducción a estadística:
Vídeo de introducción a estadística:

Vídeo de como hacer un diagrama de barras:
No hay comentarios:
Publicar un comentario